Le schéma général

Définition des principaux concepts

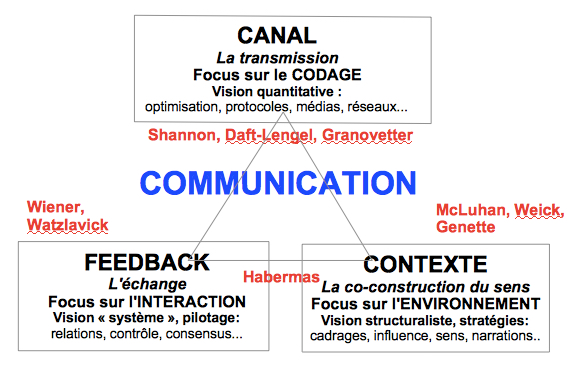
Proposée par C. Shannon et W. Weaver (voir Weaver 1949), la théorie mathématique de l’information et communication repose sur trois grands principes:

• on étudie le canal entre Émetteur et Récepteur;
• la quantité d’information est mesurable;
• le codage de l’information doit s’adapter à la capacité du canal.

En mettant ici la priorité sur l’analyse du canal de transmission, on s’oppose aux théories de la communication qui mettent en avant soit le feedback, soit le contexte social, soit le langage:

.

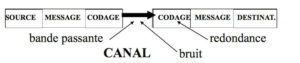
1. Émetteur et Récepteur

La situation de base correspond à un émetteur qui code un message en une série de “grains” assemblés en une séquence. L’ensemble du message comporte N éléments (les lettres de l’alphabet par exemple) qui sont envoyés dans un canal à destination d’un récepteur.

2. La mesure de l’information

Avant Shannon personne n’avait pensé que l’on pouvait quantifier une information, ni que cette quantité dépendait des probabilités d’apparition des signes (trivialement, on pourrait dire que si je sais déjà tout ce qui va être transmis par le prochain signe, alors l’information est nulle pour moi).

C. Shannon soutient sa thèse en 1940 au MIT

L’entropie H permet d’évaluer la quantité d’information maximale d’une source X en fonction de N le nombre de signes et de Pi les probabilités d’apparition de ces signes H = – (P1log1 + P2log2 + P3log3 + … + PnlogPn) Si on cherche à transmettre le maximum d’information avec le minimum de signes, alors il faudrait que tous les signes soient utilisés avec des probabilités égales. Ainsi la quantité maximale contenue au départ dans une pièce de monnaie pour jouer à pile ou face est 1 (voir le calcul ci-dessus), et la quantité maximale contenue dans un dé à 6 faces avant de jouer est 2,58 (voir Waever 1949).

3. La capacité limitée des canaux

Shannon a démontré que si la quantité d’information reste inférieure à la capacité du canal, alors les pertes tendent vers zéro en l’absence de bruit (car on peut alors trouver un code tel que la probabilité d’erreur lors de la transmission soit aussi faible que l’on veut). Pour le codage d’un alphabet par exemple, la stratégie intuitive de base consiste à attribuer des codes courts aux lettres fréquentes, et des codes longs aux lettres moins fréquentes : dès 1830, dans le codage du Morse pour la télégraphie, le E était un “point”, le T était un « trait”, mais le Y était “trait-point-trait-trait”.

L’importance des concepts développés par C. Shannon et W. Weaver est considérable, car c’est cette analyse quantitative de l’information qui est à l’origine de la notion de bande passante dans un canal, de tous les algorithmes de codage (JPEG, MPEG…) et des protocoles pour la transmission des données par Internet (TCP-IP, HTTP, FTP…) et par la téléphonie mobile (réseaux sans fil, GSM, 4G, 5G…).

Pour aller plus loin et en passant par un moteur de recherche, on trouvera  bien sûr de nombreux sites qui présentent la théorie de C. Shannon. En revanche on ne trouvera pas facilement la très bonne conférence de Josselin Garnier, qui part de l’histoire vers 1940 et va jusqu’aux développements actuels sur la modélisation du bruit (durée 1 heure + questions, niveau mathématique de Terminale, voir ce lien sur Viméo). Et si on veut replacer la théorie de Shannon parmi les autres théories mathématiques de l’information, voir cette contribution de J-P Delahaye sur le site Intersctices.

4. La discussion de la théorie mathématique de l’information

La théorie mathématique de C. Shannon limite son analyse à un messager dont la fonction est de transférer un objet-information (sous forme d’une série de “grains” assemblés en séquence probabiliste). Elle est conceptuellement indifférente à la signification du message (voir les explications de W. Weaver, 1949, partie 3) et elle est alors souvent considérée comme simpliste dans la communication organisationnelle (voir Juignet 2015) par rapport aux théories de la communication vue comme un échange dans une relation ou vue comme une construction sociale de sens.

• On retrouve pourtant les concepts de Shannon en psychologie cognitive (voir Ramel 2012, Heurley 2013), notamment pour définir les limitations de la capacité humaine de traitement de l’information (le nombre “magique” de Miller : 7 +/- 2, lien) ou pour analyser les processus de mémorisation à court terme et long terme ( voir la théorie de B. Broadbent, lien).
• On retrouve aussi l’idée d’une optimisation à rechercher entre le message et le canal dans la Théorie de la richesse des médias (voir ici le schéma 2 et voir Daft et Lengel 1986). On considère alors l’équivoque du message à transmettre et les différents canaux sont classés selon un continuum, du plus ”riche” au plus ”pauvre” (selon la vitesse de réaction, la variété des canaux disponibles, la personnalisation, la richesse du langage): le manager “rationnel” préférera choisir le canal dont la richesse perçue (depuis le SMS … jusqu’au face-à-face) correspond au mieux à l’équivoque perçue du message à transmettre (pour fixer l’heure d’une réunion, il suffira d’un sondage en ligne sur Framadate…. pour préparer les arguments à présenter, il faudra des réunions de travail préparatoires).

• Même si la théorie de Shannon n’est qu’une théorie du contenu en information (relativement à un but de compression et à une certaine distribution probabiliste des suites de caractères), on retrouve surtout l’idée de l’importance considérable des caractéristiques du canal et du codage dans la compréhension des nouvelles formes possibles de la communication sur le Web (nombre de caractères d’un Tweet, codage des photos et vidéos, flux RRS… voir Analyse des réseaux sociaux) et dans les nouvelles formes possibles de la téléphonie mobile (réseaux sans fil, protocole 5G, Internet des Objets…  voir la contribution de G. Lachaud sur le site Interstices.
• et comme l’explique W. Weaver (1949, chap. 3) en distinguant bien les trois niveaux de problèmes de la communication (A technique, B sémantique et C efficacité) : « the theory treated by Shannon, although ostensibly applicable ONLY to Level A problems, actually is helpful and suggestive for the level B and C problems« . Voir alors par exemple la Théorie des Genres de communication.

.

Voir les autres théories utilisées dans le développement des SI

Voir la carte générale des théories en management des S.I.