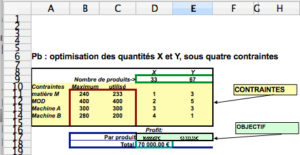
Programmation linéaire sous contraintes (le Solveur de OpenOffice)
.
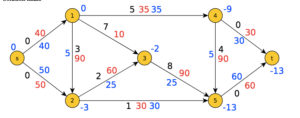Algorithme de flots de coûts minimum ( in De Smet et Fortz, 2013)
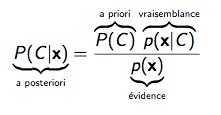Formule de Bayes : probabilité conditionnelle / probabilité totale (in Gagné 2016)
.
Définition des principaux concepts
Recherche opérationnelle, calculs de probabilités, classification automatique… la vision mathématique de la décision ne considère que l’aspect calculatoire de la rationalité (problem solving plutôt que problem finding, voir alors la critique de H. Simon). On ne se focalise en effet ici que sur la phase de modélisation-simulation (voir une bonne série d’articles de base sur le site Interstices) ou sur la phase de choix (décision en univers incertain, classification, choix multi-critères…):
- la recherche opérationnelle a pour objectif l’aide à l‘optimisation par une modélisation mathématique de problèmes courants;
- le calcul de probabilités a pour objectif l’aide au choix dans les situations de risques calculables;
- les méthodes de classement ont pour pour objectif de résoudre les dilemmes de choix, qu’ils soient sur un critère, multi-critères ou collectifs;
- la classification automatique est à la base des nouvelles méthodes utilisées en informatique : fouille de données, analyse textuelle, Intelligence artificielle… (voir aussi Intelligence artificielle et modèles de décision).
On trouve une bonne présentation de toutes ces approches mathématiques de la décision dans la partie II de Montmain et Penalva (2003). Pour avoir une vision de l’histoire de l’aide à la décision, voir Tsoukiàs (2006). Pour comprendre et tester les méthodes d’analyse de données, voir la revue Modulad soutenue par l’INRIA (notes, tutoriels, articles…).
1. La recherche opérationnelle : optimisation, théorie des graphes, programmation linéaire
La recherche opérationnelle (R.O.) s’est développée depuis la seconde guerre mondiale, quand l’armée fit appel à des équipes de mathématiciens pour résoudre des problèmes de choix militaires (organisation de convois maritimes, organisation de réseaux de radars…).
-
La théorie des graphes étudie sous forme d’arbres les chemins possibles à travers un réseau constitué de sommets reliés par des d’arêtes (un document : voir en latin la résolution du célèbre problème des sept ponts de Königsberg, par L. Euler en 1759) : algorithmes du meilleur « flot » dans un graphe, problèmes d’ordonnancement de tâches, de réseaux de transport, de chemin optimal PERT, de planning, d’optimisation de flux… voir De Smet et Fortz (2013).
-
La programmation linéaire est utilisée pour les problèmes d’affectation, il s’agit de maximiser une fonction objectif en respectant des contraintes de ressources : résolution de systèmes d’équations et d’inéquations linéaires, méthode du simplexe… Voir Fortz (2013) et voir Montmain et Penalva (2003).
2. Le calcul des probabilités : la décision bayésienne, les files d’attente, la simulation
L’aide à la décision en univers incertain est basée sur le calcul de probabilités.
-
Dans la théorie bayésienne de la décision (voir Lecoutre 2007), l’objectif est de choisir l’action qui maximise l’espérance de gains en fonction des probabilités sur « l’état du monde ». On considère ici que nos décisions combinent un calcul des probabilités avec une estimation de la valeur probable et des conséquences de nos choix (probabilité conditionnelle / probabilité totale : si je choisis le café plutôt que le chocolat qui a une probabilité p de donner la migraine, je dois reconsidérer mon choix en apprenant que le café est aussi un antidépresseur avec une probabilité p’). Pour une introduction intuitive à la démarche bayésienne, voir le cours de E. Grenier (2011) avec le cas de l’estimation d’une proportion avec Excel. Sur les modèles bayésiens, voir le cours de Gagné (2016) et le cours de Honeine et Labadi (2013). Sur les mécanismes d’inférence et les implications en Neurosciences cognitives, voir Dehaene (2012). Sur la théorie des perspectives (D. Kahneman) voir Économie comportementale.
-
La théorie des files d’attente modélise par des lois de probabilités (Gauss, Poisson, Exponentielle…) les fréquences d’arrivée des clients dans une queue et les temps d’exécution d’un service rendu par le fournisseur. Voir le cours de Gagné (2017) et ce diaporama de d’A. Blondin-Massé (2014).
-
La simulation de Monte-Carlo, quand on ne connait pas une loi probabilité, consiste à simuler un échantillon pseudo-aléatoire qui respecte les densités de fréquences connues dans le passé. Sur cet échantillon fictif on peut alors faire une approximation de l’espérance mathématique ou bien se contenter de tester plusieurs choix possibles Voir cet exercice simple de gestion de stock sur OpenOffice Calc et voir l’utilisation d’Excel pour générer des échantillons pseudo-aléatoires (E. Grenier 2006). Voir aussi les possibilités de la simulation de Monte-Carlo dans l’exemple du jeu de Go sur le site Interstices.
3. Les méthodes de classement : critères de choix, choix multi-critères, choix collectifs
Même en ne considérant que la rationalité calculatoire au niveau du choix, il reste encore de nombreux critères possibles (voir Espinasse 2009). Par exemple si on envisage plusieurs alternatives, chiffrées dans différentes hypothèses :
- selon le critère de Laplace il est raisonnable de considérer les éventualités comme équiprobables si on a peu d’information, il faut alors adopter l’alternative qui rapporte « le meilleur » des résultats (par une moyenne arithmétique dans chacune des hypothèses) ;
- selon le critère MiniMax, dit critère de Wald, il faut minimiser les pertes maximales, c’est l’option pessimiste. Pour chaque alternative on envisage les plus mauvaises conditions de réalisation et on choisi « la moins pire », l’alternative qui coûterait le moins;
- selon le critère de Savage, on construit une matrice des regrets : pour chaque alternative et dans chaque hypothèse, on affecte un regret calculé comme un manque à gagner (différence entre le résultat qui aurait pu être obtenu dans la meilleure hypothèse possible et le résultat de l’hypothèse sélectionnée). C’est sur ces regrets qu’on applique alors le critère MiniMax : il s’agit ici de regretter le moins possible mais dans le pire des cas ;
- selon le critère de l’espérance mathématique, il faut affecter une probabilité de réalisation aux différentes alternatives (par analyse ou par sentiment personnel) et faire alors un calcul de moyenne, pondérée par ces probabilités subjectives. Le meilleur choix serait donc celui qui obtient le meilleur rapport résultats/chances de réussite.
Les méthodes de choix multicritères dépassent la simple analyse coûts/bénéfices d’une fonction économique unique : en réalité il y a rarement un seul critère et lorsqu’il y a plusieurs objectifs il est impossible de les atteindre tous à la fois. B. Roy parle alors d’une « approche du surclassement de synthèse, acceptant l’incomparabilité » : on ne peut comparer les alternatives que deux à deux et on vérifie si, selon certaines conditions préétablies, l’une des deux alternatives surclasse l’autre et à quel degré. On tente ensuite une synthèse à partir de toutes ces comparaisons multiples (Montmain et Penalva, 2003). Voir cet entretien avec B. Roy, spécialiste de cette discipline, et voir cet article Wikipédia.
La théorie des choix collectifs a pour objectif d’agréger un ensemble de préférences individuelles en un ensemble de préférences sociales : classement des candidats à une élection, classement global de différents projets, réponse à un appel d’offre…
- à la suite du paradoxe de Condorcet sur la transitivité des choix individuels mais sur la non-transitivité d’une majorité (A>B, B>C… mais C>A) et sous l’hypothèse que les individus n’expriment que des préférences (un simple classement, mais sans notations), le théorème de K. Arrow (voir Fleurbaey, 2000) démontre l’impossibilité d’une procédure d’évaluation collective qui respecterait les quatre conditions : universalité (absence de restriction pour chacun), non-dictature (pas d’imposition par un individu), unanimité (une option unanimement préférée est collectivement classée devant), indifférence aux options non pertinentes (choix entre A et B, sans option sur C). Il y aura donc toujours des situations problématiques et aucune règle de vote n’échappe à la critique;
- en analysant notamment les élections aux USA, D. Saari (voir Merlin 2003) montre que traiter les problèmes séparément (paire par paire) fait perdre des informations dans le processus d’agrégation de données : il faudrait garder une trace de la rationalité des individus dans le processus d’agrégation et cela serait possible avec les classements par points. Voir aussi la proposition « à voix multiples » de K. Janeček dans ParisTech Review.
4. La classification automatique, pour la fouille de données
Dans la fouille de données ou Datamining, on cherche des structures particulières sur un large échantillon, ce qui peut permettre de faire apparaitre des relations et donc de faire des prévisions: déclencher une alerte suivant certains signaux reçus par des capteurs, accorder un prêt bancaire suivant la classe d’appartenance d’un client, détecter une fraude suivant certaines anomalies… Les méthodes de classification automatique ont pour but d’identifier les classes auxquelles appartiennent des données (objets, individus, images, textes…) à partir de certains traits descriptifs. On parle de régression quand les variables sont quantitatives et de clustering quand les variables sont qualitatives.
- Dans la classification supervisée toutes les observations doivent d’abord être « étiquetées » selon un ensemble d’attributs (par exemple pour un patient, des symptômes et des mesures) et le classement automatique consiste à attribuer une classe à chaque observation. L’analyse factorielle discriminante (AFD) prédit l’appartenance d’une observation à une classe en fonction de variables latentes, formées par des combinaisons linéaires des variables prédictives de départ. La classification ascendante hiérarchique (CAH) classe les observations par un algorithme itératif en partant de l’ensemble de ces observations (à chaque étape, une nouvelle partition agrège les classes « proches » déterminées lors de la partition obtenue à l’étape précédente).
- Dans la classification non supervisée les observations ne sont pas préalablement étiquetées. Ici nous sommes plutôt en « apprentissage peu supervisé », puisqu’on cherche d’abord à déterminer automatiquement des paramètres discriminants d’une bonne segmentation sur des données d’entrainement (à partir du choix de variables cibles), ce qui permettra ensuite de prédire les valeurs de ces cibles pour les nouveaux arrivants (par exemple pour détecter une anomalie, une faille, une fraude…). Dans la méthode des k plus proches voisins (k-NN k-nearest neighbor) on attribue à une nouvelle observation la même classe que celle des k plus proches observations qui appartiennent à l’ensemble initial (« les plus proches » sont définies avec une fonction de distance et « la même classe« est par exemple la classe majoritaire, voir cet exemple). Dans la méthode des k-moyennes (k-means, nuées dynamiques) le partitionnement par agrégation se fait autour de centres mobiles (distance d’un point à la moyenne des points de son groupe). Dans la méthode des forêts d’arbres de décision on descend dans un arbre des règles selon les réponses à différents tests pour l’observation considérée, mais il s’agit de choisir automatiquement les tests à chaque nœud ainsi que l’élagage optimal de l’arbre; CART est un des algorithmes les plus connus, voir aussi l’article Wikipedia.
- Sur les modèles informatiques de la décision, voir Intelligence artificielle et modèles de décision.
.
Voir les autres théories utilisées dans le développement des SI
Voir la carte générale des théories en management des S.I.
-
RÉFÉRENCES
J. Montmain, J-M Penalva (2003), Choix publics stratégiques et systèmes sociaux, état de l’art sur les théories de la décision, 244 pages, Mines d’Alès- CEA
Tsoukias A. (2006), De la théorie de la décision à l’aide à la décision, l’histoire critique de la R.O.
De Smet Y., Fortz B. (2013), Algorithmique et Recherche Opérationnelle
Fortz B. (2013), Applications de la programmation linéaire
Honeine P., Labadi N. (2013), Outils d’aide à la décision, un diaporama de cours (CNRS, UTT)
Lecoutre B. (2007), L’inférence bayesienne pour l’analyse des données expérimentales, Revue Modulab n° 35
Gagné C. (2016), Théorie bayésienne de la décision, Apprentissage et reconnaissance, Cours à l’Université Laval
Gagné C. (2017), Théorie des files d’attente, Cours à l’Université Laval
Grenier E. (2006) La simulation probabiliste avec Excel , Revue Modulab n°34
Grenier E. (2011) Introduction intuitive à la démarche bayésienne, Revue Modulab n°43
Dehaene S. (2012), Le cerveau statisticien : la révolution Bayésienne en sciences cognitives, Collège de France, 10 janvier 2012
Espinasse B. (2009), Analyse de la décision dans l’incertain
Fleurbaey M. (2000), Choix social : une difficulté et de multiples possibilités. Revue économique, volume 51, n°5
Merlin V. (2003), La théorie des choix collectifs à portée de tous ! Commentaires sur quatre livres de vulgarisation de Donald Saari, Mathématiques et sciences humaines